1. Introduction
The Philippi Sundial is one of the most beautiful and elegant technological artefacts and measurement devices of the Hellenic world. The Philippi Sundial is an original gadget, a portable pocket ring sundial, which encapsulates the scientific spirit and the technological innovation of the Hellenistic era. The Horologion is currently displayed at the Museum of Kavala, Greece.
A sundial is a device that indicates time by using a light spot or shadow cast, by the position of the Sun on a reference scale. Sundials have been invented independently in every major culture and became more accurate and sophisticated as each culture developed. Expectedly, within the noosphere born in the Hellenistic era (with Alexandria as its most important centre), ancient Greeks were well-positioned to develop the science (principles and forms) of sundials, having developed the science of geometry, particularly discovering the conic sections to be traced by a sundial nodus. The portable Horologion of Philippi is one of the finds from the archaeological excavation in the Octagon church of Philippi in Macedonia, Greece, which exhibits clear-cut functionality combined with unprecedented ergonomic design. Its distinctive type renders it unique, since it does resemble common elements, but significantly differs from, the three main types of sundials developed through the science of gnomonics of the Hellenic world. The user of the Horologion of Philippi could not only read the local hour in the region (latitude) of four cities but also calculate the latitude of a specific place, as well as the horizontal coordinates (that is the azimuth and the altitude of the Sun or another celestial object). Based on analyses of its epigraphic evidence, archaeologists date the construction of the Horologion of Philippi between 250 and 350 C.E.
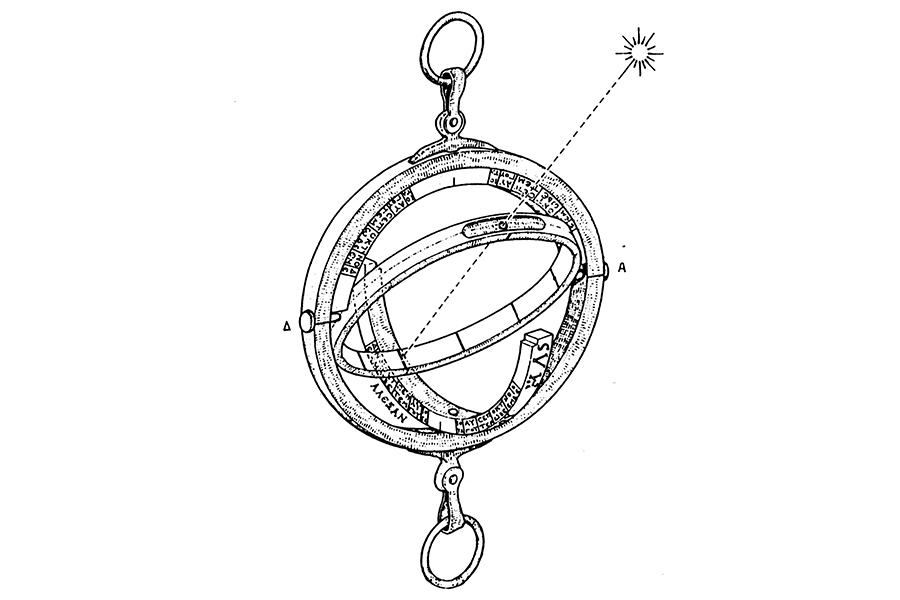
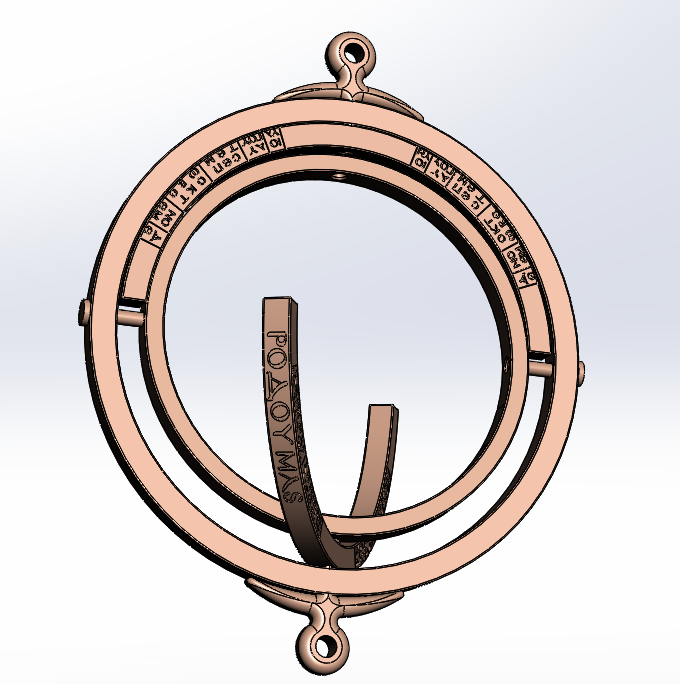
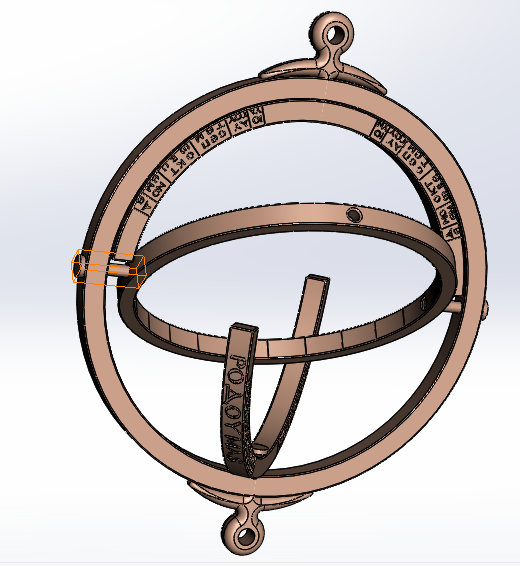
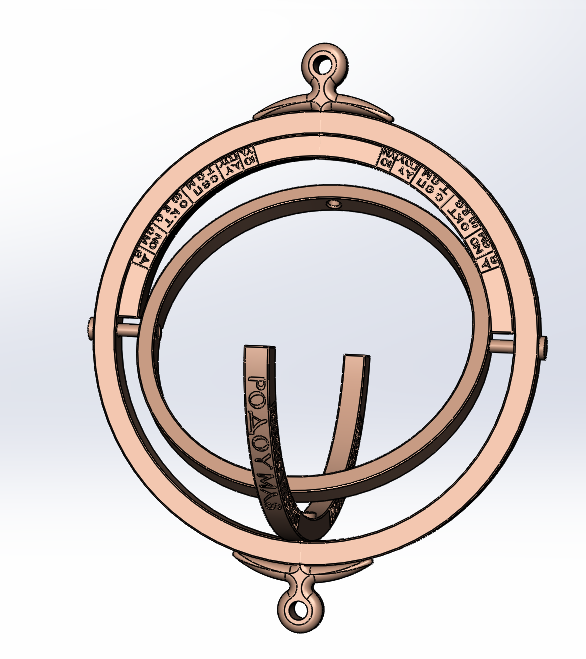
The Horologion of Philippi is a circular object made of copper alloy (around 72.5 mm in diameter), consisting of three rings placed inside each other. The inner ring carries an optometric (view) hole aiming at the sun, while the middle ring is made of two half rings, each bearing various engravings bilaterally, from the centre to the edges.
The first (outer) ring has an inner diameter of 64.9 mm, 3.8 mm thick, and 5 mm wide. It has no engraving or inscription, other than the holes for the shafts holding the other rings.
The two separate half-rings, which comprise the middle ring, have an external diameter of 64.5 mm, an inner diameter of 57.2 mm, a thickness of 3.6 mm, and a width of 5 mm. They are constrained by an axis placed as a mono-block construction, with the stem through which the hoop passes allowing for complete (360°) rotation. On the outer cylindrical surface of each
semicircle, a pair of city names followed by their corresponding latitudes are engraved; Alexandria, Egypt, 31° and Rhodes, Greece, 36° on one, and Vienne, France, 45° and Rome, Italy, 41° on the other. On each flat side of the hemisphere, months Jan-Jun and Jul-Dec are engraved respectively, with indications laid out counterclockwise across 47° arcs (twice the 23.5° ecliptic tilt of the earth).
The third (inner) ring has an outer diameter of 57 mm, an inner diameter of 51.5 mm, a thickness of 2.8 mm, and a width of 5 mm and can rotate around a fixed axis (constrained in the outer ring) with the help of two diametrically opposed pins, obtaining a gimbal suspension.
Utilities and Operation
Finding the local time
The Philippi sundial’s unique ergonomic form makes it appropriate for a variety of uses. The sundial’s user discovers the current local time in the four cities’ vicinity, the latitude of a certain location, and the horizontal coordinates, or azimuth and altitude of the Sun or another celestial object. It can be employed as an astronomical instrument for observation as well as a time measurement device and a terrestrial system for determining location.
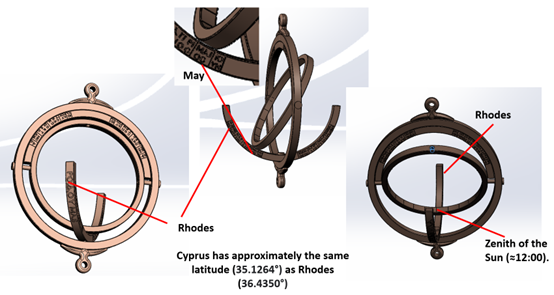
Finding the latitude
The Philippi Sundial’s user measures the height of the Sun over the astronomical horizon on the day of the equinox after setting the instrument in the working position, which entails mounting it towards the location’s zenith and orienting the outer ring perpendicular to the meridian plane. The complement of the place’s latitude is equal to the height of the Sun.
Finding the azimuth and altitude of a celestial object
The outer ring is placed in the meridian plane, the middle ring in the east-west plane, and the inner ring is used as the horizon circle by the clock’s user. The user can determine the azimuth and altitude of the celestial object by aiming at it.
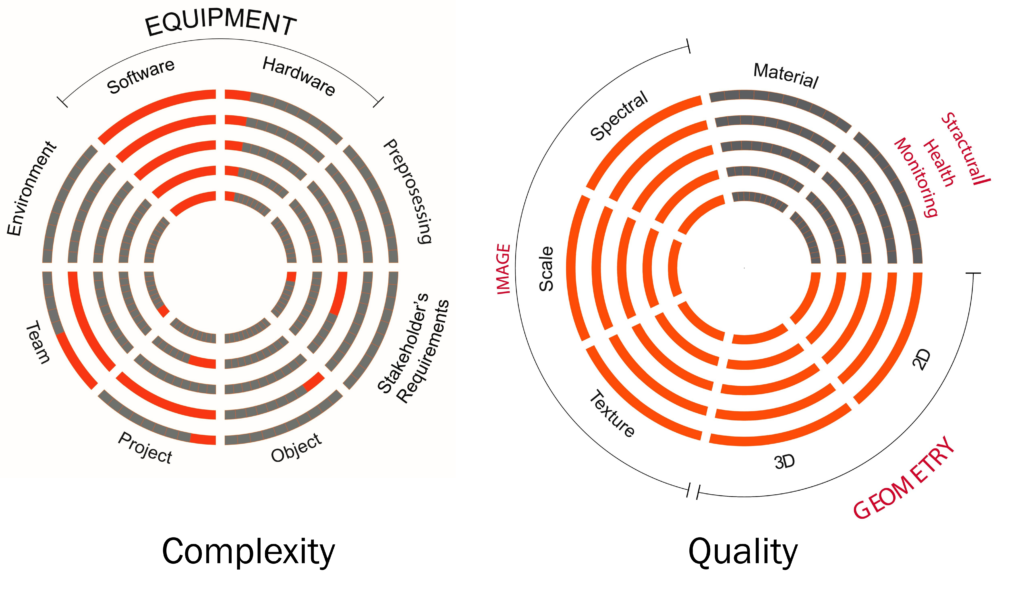
3. Estimation of Complexity & Quality
The following radial charts are base on the based on the EU 3D Study/VIGIE 2020/654
4. Taxonomy
This is a top-level view, clicking on the image will open up the full taxonomy in a new window
6. Research Outputs
Creating the 3D Geometry
For the 3D Geometry of the object, the MNEMOSYNE team worked with the Department of Mechanical Engineering of the Aristotle University of Thessaloniki and with the assistance of the data that were collected and the photographs of the prototype from the museum, under the supervision of the Era chair, the object was designed in 3D form by the partners of the department of Mechanical Engineering of the Aristotle University of Thessaloniki, using the appropriate software and more specifically the Computer Aided Design System (CAD).
Using CAD, virtual testing of the object’s utility and operations was conducted. With the help of the processed photos, a three-dimensional model was created with the assistance of the software ‘Agisoft Metashape’, of which the following sundial angles can be seen. After its completion and after the object’s utility was inspected, the necessary information and data were generated for the creation of a true, functional, physical replica of the sundial.
Using the replica of the Horologion of Philippi
Presentations & Posters
Videos
Accessibility and Reuse
This case study has been submitted to the local aggregator (APSIDA) and successfully harvested into the Europeana platform under CC BY-NC-SA 4.0 license.
7. Bibliography
- A. Basiakoulis, M. Efstathiou, K. Efstathiou, M. Anastasiou, J.H. Seiradakis “Ancient technology – The calculation of the equation of time with the use of a cam mechanism”
- Duffett-Smith, P., (1995), “Practical Astronomy with your Calculator”, 3rd Edition, Cambridge University Press.
- U S Nautical Almanac Office (2011), “The Astronomical Almanac for the Year 2011”, Section C2.
- Ptolemy Claudius (ca. 150 BC), “Almagest”, III, 9.
- Evans, J., (1998), “History and Practice of Ancient Astronomy”, Cambridge Univ. Press, New York).
- Neugebauer, O., (1975), “ A History of Ancient Mathematical Astronomy”, Springer, New York.
- Evans, J., (1998), “History and Practice of Ancient Astronomy”, Cambridge Univ. Press, New York).
- Stahlman, W.D. , Ph.D, (1960), “The Astronomical Tables of Codex Vaticanus Graecus 1291”, Brown University.
- Geminus, (ca. 50 BC), “Introduction to the Phenomena”, VI, 1-4.
- Jones, L., (December 2005). “The Sundial and Geometry”. North American Sundial Society. 12 (4).
- W. Sawyer F., Bifilar gnomonics, JBAA (Journal of the British Astronomical Association), 88(4):334–351, 1978
- Rohr, R.R.J., Sundials: History, Theory, and Practice. Toronto: University of Toronto Press, undated
- Marshall, R.K., Sundials. New York: the MacMillan Company, 1963.
- Gounaris, G., Χάλκινο Φορητό Ηλιακό Ωρολόγιο από τους Φιλίππους, (Bronze Portable Sundial from Philippi, in Greek), Αρχαιολογική Εταιρεία, (Ανάτυπο από την “Αρχαιολογική Εφημερίς”), Αρχαιολογική Εφημερίς, (1978) 181-191.
