1. Introduction
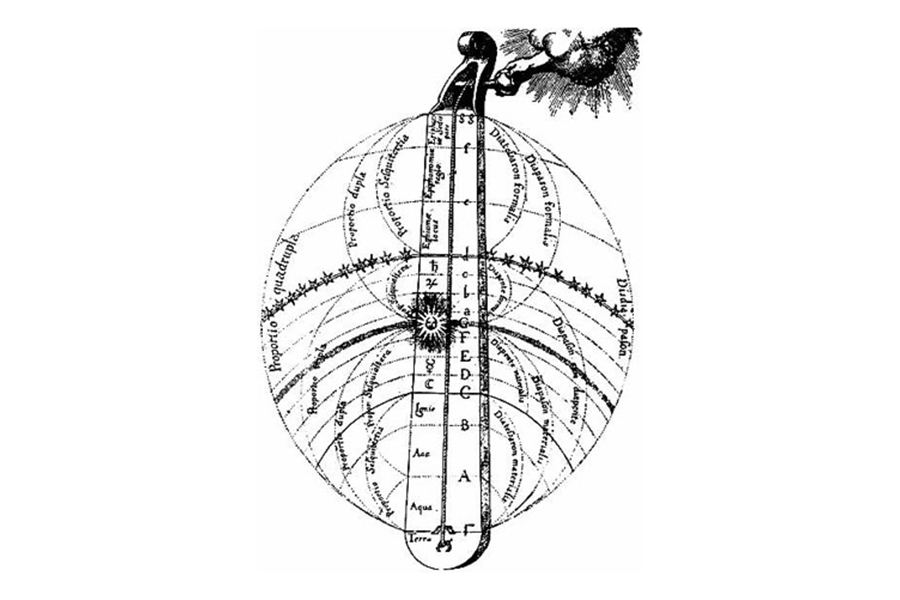
A monochord, also known as a single-stringed sonometer, is an ancient musical and scientific laboratory instrument, involving one (mono-) string (chord), upon which points may be delineated to signify where the string must be stopped to give certain notes, allowing comparisons. The string is fixed at both ends and stretched over a sound box. One or more movable bridges (tasta) are then manipulated to demonstrate mathematical relationships among the frequencies produced. “With its single string, movable bridge and graduated rule, the monochord (Kanōn [Greek: rule]) straddled the gap between notes and numbers, intervals and ratios, sense-perception and mathematical reason.” Music, Numeracy and Astronomy were inexorably linked to it, at the time.
This one-string zither finds its oldest known written trace in the Division of the Kanōn (probably by Euclid). It is described as a long hollow wooden box along the top of which is stretched one string, rigidly attached to the box at one end, with provision at the other for changing the tension. As such, it could be used for studying audible changes in pitch (fractions above/below some fixed original frequency), as well as showing that frequency varies inversely as the length (or as the square root of the mass per unit length) of the vibrating string, or directly as the square root of its tension. Although somewhat simple in its conceptualization, the intangibility aspect distinguishes this case study from the rest. No concrete evidence about the actual dimensions or materials has been found so far, however, a lot can be inferred from the way ancient Greeks managed to transform the auditory experience into visual perception; namely acoustical axioms, pure mathematical propositions, and a series of corollaries relating notes within the Greater Perfect System. This means we needed to trace manufacturing trends back to the Pythagorean Era and collect evidence from third-party descriptions whenever the Kanon is mentioned (keeping an eye out for human biases, accounting for the Pythagoreanism evolving into a cosmology theory with religious and cult extensions.).
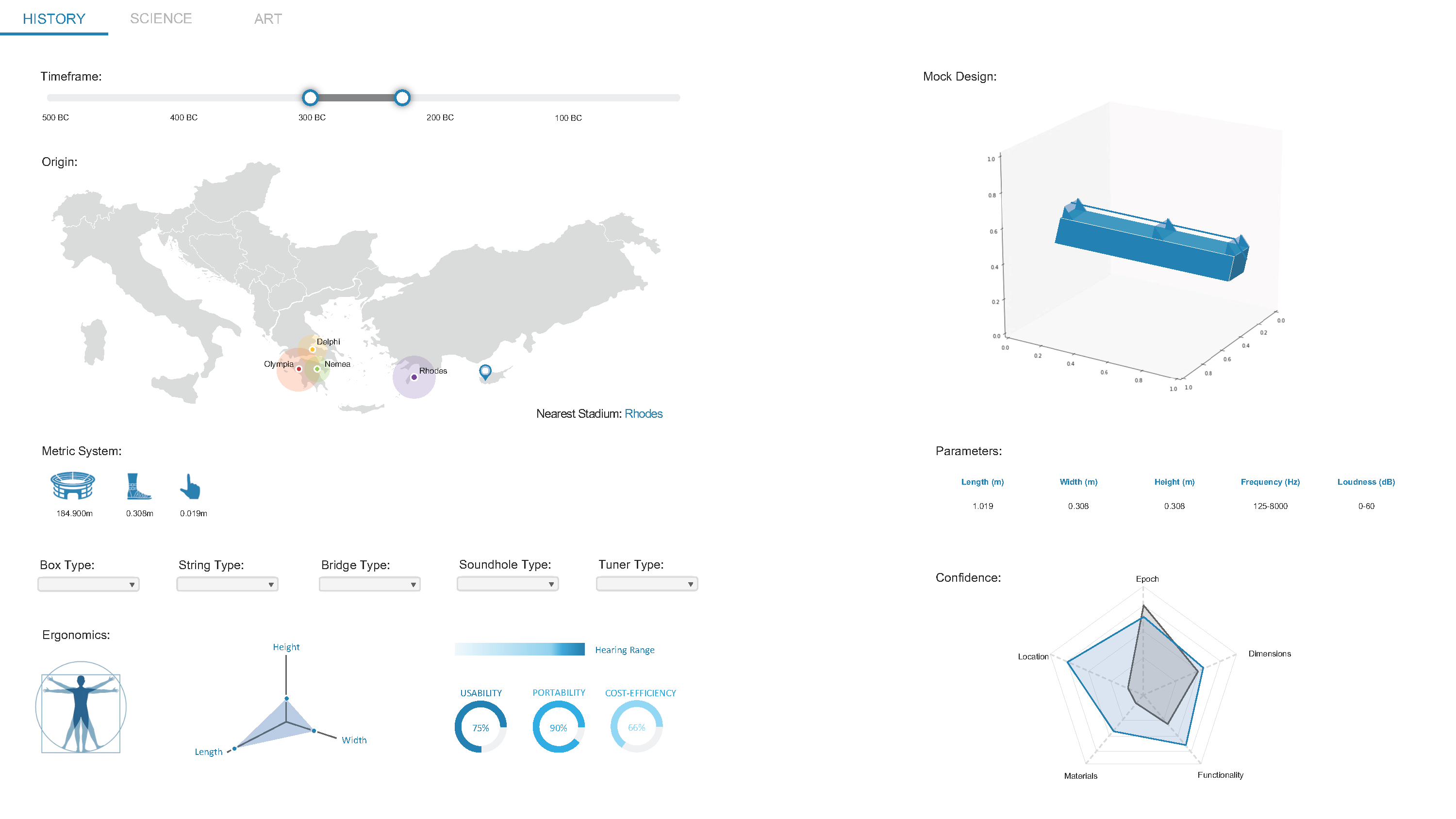
The team intends to apply an innovative (user-driven) approach for the first time. That is, build an EdTech interactive software tool with an open (customizable) frontend configuration, where the user essentially becomes the designer. In the first instance, our interface will allow for controlled parametrization, allowing the user to tune several adjustable metrics (such as dimensions, materials, etc.) and come up with their version of the monochord (along with some estimated probability measure of confidence in its description accuracy). Afterwards, the resulting 3D model will be capable of offering highly engaging (non-immersive) digital experiences, relying on sensory stimuli to bring DCH to life. This means emphasis will be placed on adaptation/personalization of the learning experience (LX) fueled by drive-time calculations.
The speciality of this Case Study lies in the fact that it is an ancient object for which we only have basic information from the Ancient Greek Grammar, but not of the physical object nor the corresponding drawings. Based only on written information from ancient times and information from modern literature expressing various opinions about the Kanon, one of the main goals is to design the possible structure of the object (digital 3D geometry).
Another goal is to find out how such an object can be used as a tool in education. For example, with the implementation of the appropriate application that can be used for teaching purposes. In this manner, the Kanon can be used as an educational tool in the areas of Music, Mathematics, and Physics.
3. Estimation of Complexity & Quality
The EU 3D Study/VIGIE 2020/654 does not support pure “Born Digital” objects and can not be meaningfully applied to such digital artefacts. DHRLab is continuing to investigate what would be necessary to accommodate Born Digital objects into a Complexity and Quality assessment.
4. Taxonomy
This is a top-level view, clicking on the image will open up the full taxonomy in a new window
6. Research Outputs
Prototype Digital Application
7. Bibliography
- Paxson, T. D. (1985). Art and Paideia. Journal of Aesthetic Education, 19(1), 67-78.
- Barker, A. (2007). The science of harmonics in classical Greece.
- Stanulonis, C. Pythagoras the Musician (Doctoral dissertation).
- Huffman, C. (2006). Pythagoreanism.
- Caleon, I., & Ramanathan, S. (2008). From music to physics: The undervalued legacy of Pythagoras. Science & Education, 17(4), 449-456.
- Gibson, S. (2016). The Science of Harmonics and Music Theory in Ancient Greece. A Companion to Science, Technology, and Medicine in Ancient Greece and Rome, 161-178.
- Saferstein, B. (1991). Resurrecting the Pythagorean monochord. The Physics Teacher, 29(7), 438-439.
- Levin, F. R. (2009). Greek reflections on the nature of music. Cambridge University Press.
- K. Efstathiou, E. C. (2022). Enriching user experience via user-centred design: a more inclusive approach to digital cultural heritage. CAA 2021
- “The Harmony of the World: 75 Years of Pythagorean Monochords” by Lloyd Rodgers (Journal of New York University Music Department, 2006).
- “The Music of Pythagoras: How an Ancient Brotherhood Cracked the Code of the Universe and Lit the Path from Antiquity to Outer Space” by Kitty Ferguson.
- “Pythagoras and the Pythagorean School” by Philip H. De Lacy and Estelle Allen De Lacy (The Classical Journal, 1917).
- “The Pythagorean Monochord” by Mark Marrington (The Musical Times, 2002).
- “The Harmonic Origins of the World: Sacred Number at the Source of Creation” by Richard Heath.
